基于PSM-DID的教育对性别收入差距的影响研究
2024-08-26   来源：杨庆芳   

性别收入差距，是衡量性别收入不平等的重要指标，反映了社会上“同工不同酬”现象。它是世界上每一个国家都存在的一个问题，因此从性别角度看待收入差距的研究是国内外关注的重点课题。改革开放后，我国不断出台各种有利于女性群体的法律法规以及相关政策，旨在提升女性的收入水平，缩小男性和女性收入差距，实现收入公平。由于历史遗留因素，我国存在一定的重男轻女思想，从而导致我国具有显著的性别收入差距。尽管我国居民工资水平不断增长，但2021年男性的平均月薪是女性的1.3倍。我国要实现收入平等、全面小康的目标，性别收入差距是必须解决的一个问题。

根据已有的研究成果，影响性别收入差距的因素有很多，例如最低工资制度、地区文化差异、信息化水平、非认知技能、家庭环境等。在我国市场化的社会中，学者对于性别收入差距分析的角度和最后得出的结论多种多样，并没有达成一致。现阶段我国处在发展方式转型的关键时期，亟需可以稳健借鉴的研究。教育，一直是我国政府始终坚持资源倾斜的一个行业，那么，在众多的影响因素混合作用下，教育对于性别收入差距的缩小作用是否显著？是否可以通过平衡受教育程度来降低性别收入差距？这些问题都值得探究，但国内所做研究不多。现阶段国内的研究缺少教育对性别收入差距的因果效应分析，大部分是多个因素混合研究，鲜有专门研究某个等级教育对于性别收入差距的影响，因此这也是本文研究的着眼点。研究教育对于我国性别收入差距的具体影响程度，便于政府了解教育政策的施行对于缩小收入差距的量化作用，有利于不断调整教育政策以加快实现共同富裕的步伐。

现有的国内外关于性别收入差距影响因素的研究，一方面从性别歧视、职业或职位隔离、地区文化差异入手，另一方面从互联网使用、普惠金融发展、工业机器人应用1314、代际支持15、家庭环境16、生育行为17、生育政策18、公共部门发展19、最低工资制度20等方面展开分析。仅有少数学者围绕教育对性别收入差距的影响展开研究。Garcia-Prieto和Gómez-Costilla21基于来自欧盟收入和生活条件统计数据的西班牙数据，将性别工资收入差距分解为可解释的部分和不可解释的部分，且发现教育在可解释的部分中占据重要地位。韩雷和侯新望利用2013年CHIP调查数据，指出女性获得高学历才能够有效减小其与男性收入的差距。李晓光从教育与职业的匹配度入手，采用2003年至2017年的CGSS数据，探究了教育失配对性别工资差距的影响，指出女性发生教育失配的概率高于男性，由此导致更大的性别收入差距，且该现象随着时间的变化越发明显。刘杰和赵锋基于不同时期的CHNS数据，验证了女性教育回报率大于男性，且该差异在非国有部门和受教育程度较低的群体中更大。

已有研究为本文提供了诸多有益的借鉴，但仍存在一些不足之处：一是鲜有研究深入研究不同类型教育对性别收入差距的影响；二是已有研究在探究教育对性别收入差距的影响时，较少考虑样本选择偏差对估计结果的影响。因此，本文基于2015—2021年中国综合社会调查（Chinese General Social Survey，简称为CGSS）的相关数据，运用倾向得分匹配法（PSM）针对性地量化分析了中等教育和高等教育对于性别收入差距的影响作用。

（一）模型构建

本文利用Rosenbaum和Rubin于1983年提出的倾向得分匹配方法（PSM）中卡尺范围内的最近邻匹配方法和双重差分方法来探究教育对于性别收入差距的影响。传统的回归分析不能避免样本选择偏差，样本家庭环境、工作类型以及个人智力等的不同都会干扰教育对于性别收入差距的影响，从而影响到回归结果。PSM可以通过匹配到倾向值相近的控制组（没有接受相应教育程度的群组）和处理组（接受相应的教育程度的群组）克服两个群组在样本选择上的偏误，科学合理地平衡数据，从而能够更精确地查找因果关系。因为已有的混淆变量已经被综合为最终的倾向值，所以倾向值相近的处理组和控制组收入的不同就可以主要归因于是否接受相应教育，最后进行差分回归就可以找出相应教育程度对于性别收入差距的影响，进而满足本文探究教育对于性别收入差距影响的需要。换言之，PSM方法的本质是基于反事实框架进行因果关系的探究，即在探究某一干预或政策的影响时，构建处理组的反事实，如果处理组不接受干预或处理结果变量会是如何，考虑到现实生活事件的不可逆性，故在控制组中找到与处理组在混淆变量上很相似的样本作为处理组的反事实事件，从而控制混淆变量对于所研究问题的影响，使得匹配到的处理组和控制组在探究的指标上更具有可比性，由此得到的处理组和控制组在结果变量上的不同即某一干预的净影响。

卡尺范围内的最近邻匹配法是应用较多的一种匹配方法，结合了最近邻匹配和卡尺匹配。根据本文的数据特征，将卡尺设为0.03，即接受相应教育程度的群组和没有接受相应教育程度的群组的倾向值的差值的绝对值落在该卡尺范围内才会被留下，即仅当处理组和控制组的p值满足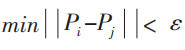，样本才会被保留下来。在进行匹配的过程中，要将多个控制变量通过下式中的函数计算得出一个数值（倾向得分数值），即每个样本接受相应教育程度的概率如下。

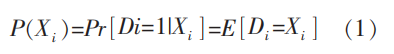
在本文中，倾向得分数值反映的是样本个体接受相应教育的概率，同时，它亦是混淆变量的函数，故简称为P（Xi），而作为指示变量，样本个体处于处理组时等于1，处于控制组时等于0。在进行匹配后，可以利用（2）式计算出男女性别收入差距并对比分析接受相应教育和未接受相应教育样本性别收入差距的不同，从而探究相应教育对于性别收入差距的平均影响作用。

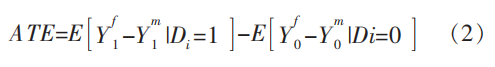
其中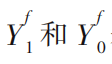，表示同一男性在接受相应教育和没有接受相应教育两种状态下的收入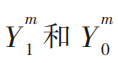，表示同一女性在接受相应教育和没有接受相应教育两种状态下的收入。

本文对于所研究问题的分析共有以下四个步骤。

第一，计算倾向得分数值。这一步利用Logistic参数模型对混淆变量进行计算，得出每个样本个体接受中等教育和接受高等教育的概率。

第二，基于倾向值进行匹配以及匹配效果检验。基于（1）式和第一步中提到的方法对每个样本进行倾向值打分，从而每个个体都会得到一个倾向得分数值。然后利用卡尺为0.03的最近邻匹配方法将处理组和控制组的个体进行匹配。匹配完成后，需要对匹配效果进行检验，若匹配的处理组和控制组的PS值差异显著，则需要重新匹配，直到控制组和处理组的PS值差异在统计上不显著。需要注意的是，不是每个样本个体都可以找到与之匹配的个体，因为计算出来的PS值可能存在极端值，无法匹配的个体不会在最后的结果中出现。

第三，匹配后的相关检验，即均衡性检验。匹配完成后，下一步便是检查处理组和控制组成员之间的控制变量平衡性。在这一步中，我们将计算控制变量在处理组和控制组之间的均值差及显著性。若所有的差异均不显著，则匹配成功，反之，则需要重新调整匹配。

第四，进行差分回归分析。基于上文匹配成功的数据，利用Logistic模型对数据进行回归分析，从而分析相应教育对于性别收入差距的净影响进行分析。根据本文分析问题所需，构建了如（3）所示的方程，其中，Yi表示因变量——平均月收入的对数，X1表示指示变量，当研究中等教育对于性别收入差距的时候，表示是否接受中等教育，接受中等教育等于1，未接受中等教育等于0；当研究高等教育对于性别收入差距的影响时，表示是否接受高等教育，即接受高等教育等于1，未接受高等教育等于0，而则Xi表示一系列控制变量。

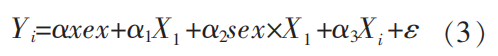
以探究高等教育对于性别收入差距的影响为例，依据上面的回归方程，接受高等教育的男性的对数月收入的对数的期望为如下。

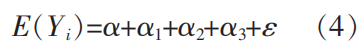
未接受高等教育的男性的对数月收入的期望为如下。

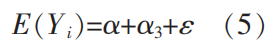
接受高等教育的女性的对数月收入的期望为如下。

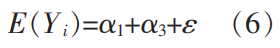
未接受高等教育的女性的对数月收入的期望为如下。

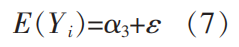
所以，接受高等教育的群体的性别收入差距的期望值为如下。

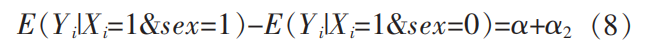
未接受高等教育的群体的性别收入差距的期望值为如下。

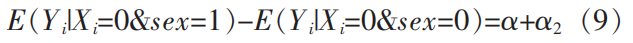
综上可得，高等教育对于性别收入差距的影响的期望值为ATE=α2。

（二）变量说明

1.被解释变量

被解释变量为个体平均月收入。因为本文所研究问题为教育对性别收入差距的影响，故将平均月收入作为被解释变量，在模型计算过程中，对其取自然对数。本文所用的收入数据为个人总收入，包括工资、奖金、补贴、利息等所有收入在内，同时，删除收入数据中不清楚回答的、拒绝回答的、被判定不适用的样本。

2.关键解释变量

关键解释变量为受教育程度，包括中等教育和高等教育。本文将最高受教育程度分为中等教育（初中及以上=1，初中以下=0）和高等教育（高中以上=1，高中及以下=0）两类，分别探讨中等教育和高等教育对于我国性别收入差距的影响。

3.控制变量

根据本文所研究的问题，控制变量为性别（男性=1，女性=0）、民族（汉族=1，其他=0）、政治面貌（党员=1，其他=0）、工作类型（全职=1，其他=0）、工作单位性质（党政机关或事业单位=1，其他=0）、管理层级（管理他人=1，其他=0）、工作经验及其平方、户口类型（非农户口=1，农业户口=0）、父母受教育程度（父母至少有一人接受高中及以上=1，其他=0）、父母单位类型变量（父母至少有一人在党政机关或事业单位=1，其他=0）。其中，借鉴已有研究的做法，通过公式“年龄-受教育年限-6”计算得到个体的工作经验。考虑到我国不同地区之间的禀赋差异较大，本文引入了地区变量，将全国分为东部地区、西部地区以及中部地区，以西部地区为基准，分别构建了东部地区变量（东部地区=1，其他地区=0）和西部地区变量（西部地区=1，其他地区=0）（表1）。

（三）数据来源

本文使用的数据来自由中国人民大学组织开展的中国综合社会调查（CGSS）2015—2021年的调查问卷，该调查起始于2003年，涵盖全国31个省、自治区、直辖市（不含港澳台）的一万多个家庭户，采用目前国内大型社会、经济调查所普遍公认的基于地图地址的抽样方法，设计方案充分考虑了全国及不同地域估计的需要，对调查总体进行了科学、细致的分层，在一定程度上提高了估计精度。样本对于研究全国范围内的问题具有很强的代表性，而且数据内容丰富，包含我国居民收入、就业、教育等变量，故采用此调查数据可以满足本文研究问题所需。在对样本进行筛选时，本文将年龄变量范围划定在18—64岁。本文所用变量的特征见表2。

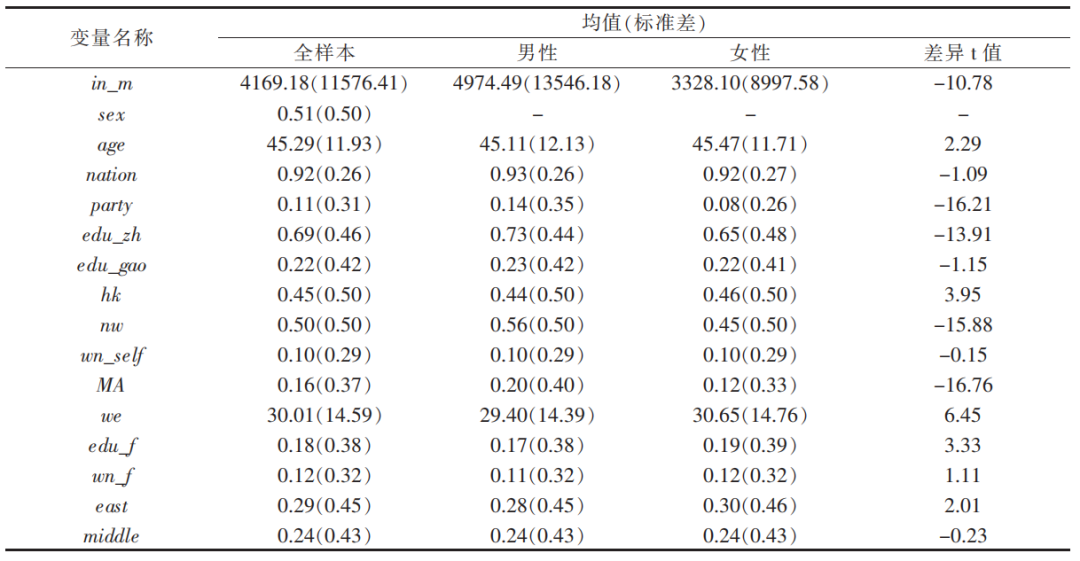
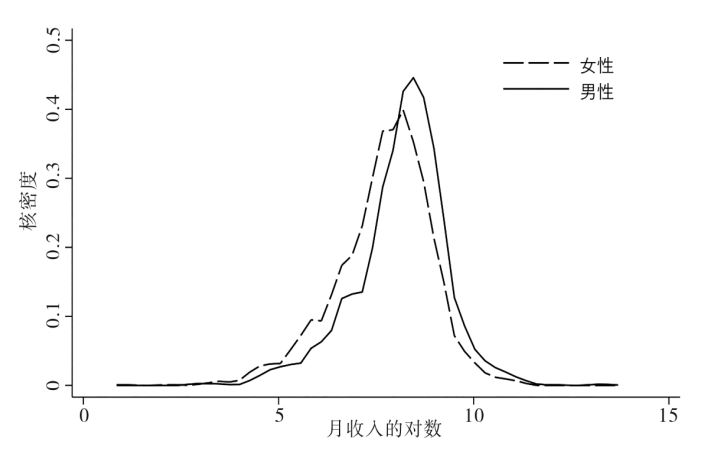
图1显示了数据经过初步处理后的男性和女性月收入对数值的核密度曲线。在图1中，当女性收入分布的曲线达到最高点之前，女性的曲线一直不低于男性的曲线，但是当女性收入分布的曲线达到最高点之后，男性的曲线就一直不低于女性的曲线，且男性收入分布图最高点所对应的收入水平要高于女性收入分布图最高点所对应的收入水平，同时所对应的密度也大于女性收入分布图最高点的密度，说明在本文所研究的群体中，男性的收入水平要更多地集中在比女性收入水平高的位置，验证了性别收入差距的存在。

（一）平衡性检验

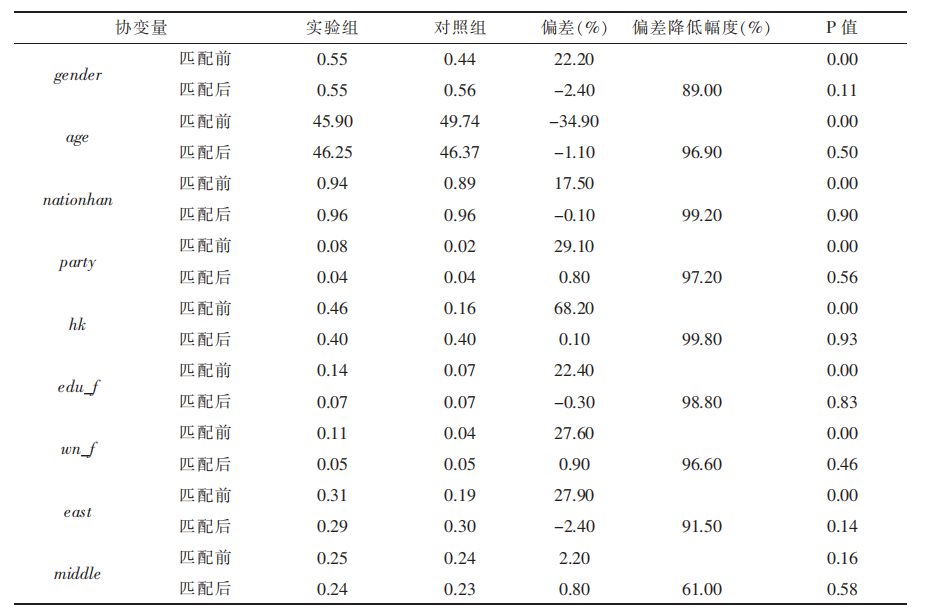
为了进一步使本文数据匹配的结果更具有说服力，对匹配前后处理组和对照组的偏差进行检验，具体如表3和图2所示。其中，表3为系列混淆变量在处理组和对照组之间的偏差进行检验，图2为匹配后处理组（接受相应程度教育）和对照组（没有接受相应程度教育）的共同支撑域图。结合表3和图2可得，匹配之后各混淆变量在处理组和对照组之间的差异均不显著，即匹配的效果较好。

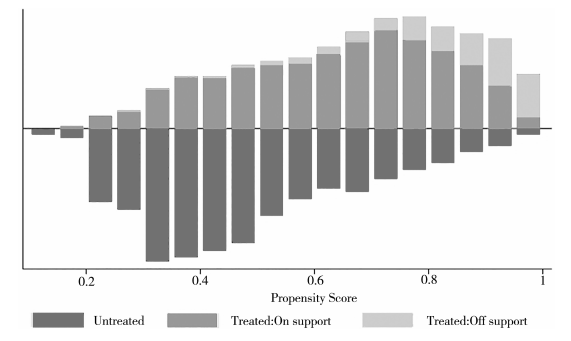
（二）倾向值匹配结果

表4展示了匹配前和匹配后样本根据（3）式回归的结果，其中，（1）和（3）表示的是探究中等教育对性别收入差距的影响的PSM匹配前和匹配后的回归结果，s_chu表示的是sex（性别）和edu_zh（是否接受中等教育）的交互项，（1）列是PSM匹配前的回归结果，（3）列是PSM匹配后的回归结果；（2）和（4）表示的是探究高等教育对性别收入差距的影响的PSM匹配前和匹配后的回归结果，s_gao表示的是sex（性别）和edu_gao（是否接受高等教育）的交叉项，（2）列是PSM匹配前的回归结果，（4）列是PSM匹配后的回归结果。又由上文分析可得，模型中交叉项的系数就是所研究的相应教育程度对于性别收入差距的效应值（见表4）。

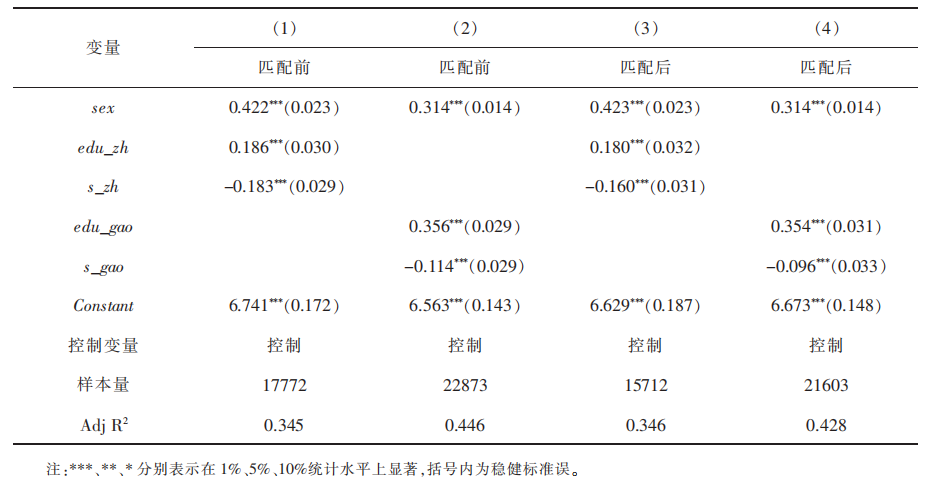
由表4中的回归结果可得，在对数据进行卡尺范围内的最近邻匹配之前，中等教育可以使得性别收入差距缩小18.3%，高等教育对于可以使得性别收入差距缩小11.4%，且都在1%的统计水平上显著；而PSM匹配后的数据回归结果显示，中等教育可以使得性别收入差距缩小16.0%，高等教育可以使得性别收入差距缩小9.6%。同时，中等教育、高等教育可以使得月收入的平均水平分别提升18.0%和35.4%。所以，在我国未来的发展过程中，要达到缩小我国性别收入差距的平均水平，中等教育和高等教育必不可少。

本文使用2015—2021年的CGSS数据，根据指示变量将数据分为处理组（接受相应教育的群组）和控制组（没有接受相应教育的群组），利用卡尺范围内最近邻在没有接受相应教育程度的群组中找出与接受相应教育程度群组匹配的样本，再进行双重差分回归，探究中等教育和高等教育对性别收入差距的净效应，得出以下两个结论。

第一，就平均水平而言，2021年我国男性月收入（4974.49元）比女性月收入（3328.10元）高出1646元，即超出女性月收入将近50%的水平，且在统计上显著。说明我国性别收入差距依然存在，同时也证明了本文研究的必要性。

第二，在男性群体和女性群体存在收入差距且差距在统计水平上显著的前提下，控制其他变量不变，中等教育和高等教育可以使得性别收入差距分别缩小16.0%和9.6%，说明女性的平均教育收益率要高于同等条件的男性的平均教育收益率，验证了教育对于缩小性别收入差距的影响作用。